Z množico v matematiki mislimo na skupek različnih objektov, ki imajo neko skupno lastnost.

Elementi množice so lahko karkoli: števila, ljudje, črke v abecedi, druge množice, itd. Množice označujemo z velikimi črkami.

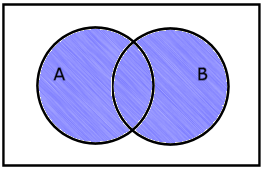
Dve množici A in B sta enaki, kadar vsebujeta natanko iste elemente.

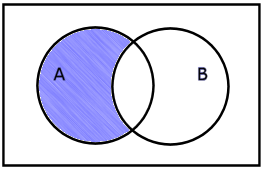
Množica A je podmnožica množice B, kadar je vsak element iz množice A tudi element množice B. To označimo z .

Unija množic A in B je množica, ki vsebuje vse elemente iz množice A in vse elemente iz množice B. Unijo množic A in B označimo z .

Matematično lahko unijo dveh množic zapišemo kot: .

Za unijo veljajo naslednje lastnosti:

Unijo dveh množic lahko ponazorimo z Vennovimi diagrami. Kroga predstavljata množici A in B, šrafiran del pa unijo obeh množic.

Presek dveh množic A in B je množica, ki vsebuje elemente, ki so hkrati v A in B. Presek množic A in B označimo z .

Matematično lahko presek dveh množic zapišemo kot: .

Za presek veljajo naslednje lastnosti:

Presek dveh množic lahko ponazorimo z Vennovimi diagrami. Šrafiran del predstavlja ravno presek množic A in B.

Presek in unijo povezujejo naslednje enačbe:

Prvima dvema lastnostma pravimo distributivnost, drugima dvema pa absorbcija.

S presekom in unijo lahko definiramo moč unije dveh množic A in B, ki nam pove število elementov v uniji. To je enako vsoti števila elementov iz A in števila elementov iz B, od katere odštejemo število elementov, ki so vsebovani tako v A kot v B. Dobimo naslednjo enačbo:

Razlika množic A in B je množica, ki vsebuje elemente iz množice A, ki niso v množici B. Razliko množice A in B označimo z . Razliko množic lahko zapišemo matematično:

Na diagramu razliko označimo kot:

Komplement množice A je množica z elementi iz univerzalne množice , ki niso v A. Komplement množice A označimo z .

Komplement lahko zapišemo kot: .

Nekatere lastnosti, ki veljajo za komplemente, so:

Veljata tudi naslednji pomembni zvezi, ki jima pravimo de Morganova zakona:

Komplement unije množic na Vennovem diagramu izgleda takole: