- Kroglico zakotalimo proti luknji, tako da pade vanjo. Pozorno si oglejte posnetek poskusa.
Vodoravni met
Vodoravni met
Timotej Maroševič
lahka srednja
10-20 min
Zakotaljena kroglica
Hitrost kroglice v vodoravni smeri
- Predpostavite, da žogica zanesljivo pade v luknjo, če se spusti za polmer, ko zadene ob nasprotno steno luknje.
- Izračunajte največjo možno hitrost žogice, da bo ta še zanesljivo padla v luknjo. Za vzemite m/s2.
m/s
Pričakujemo, da učenci vedo, da je vodoravni met sestavljeno gibanje. Za rešitev problema je potrebno izračunati čas, v katerem se kroglica spusti za polmer.
s
V tem času se kroglica premakne do desnega roba luknje in prepotuje razdaljo m. Od tod sledi hitrost m/s.
s
V tem času se kroglica premakne do desnega roba luknje in prepotuje razdaljo m. Od tod sledi hitrost m/s.
Odlično, lahko nadaljujemo.
Rezultat ni pravilen. Morda vam bo v pomoč, če si narišete skico.
Rezultat je napačen.
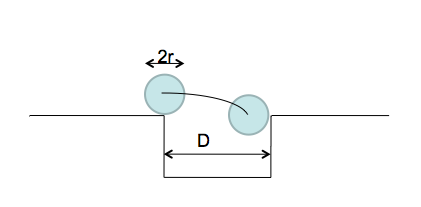
Prikazana je tirnica, po kateri se giblje kroglica, ko pada v luknjo. Širina luknje je označena z , premer kroglice pa z .
- Premer kroglice je cm, širina luknje pa cm.
Povprečna hitrost v vodoravni smeri
- S pomočjo podatkov, ki jih dobite iz zaporedja slik, določite povprečno hitrost kroglice v vodoravni smeri.
m/s
Od učencev pričakujemo, da bodo s slik znali razbrati lego in čas kroglice. Na podlagi enakih premikov morajo ugotoviti, da gre za enakomerno gibanje in izračunati hitrost.
Čas med dvema slikama je s, kroglica pa se premakne za cm. Od tod sledi hitrost m/s.
Čas med dvema slikama je s, kroglica pa se premakne za cm. Od tod sledi hitrost m/s.
Odlično! Lahko nadaljujemo.
Rezultat ni pravilen. Pravilen rezultat je m/s m/s. Nadaljujte z nalogo.
Rezultat ni pravilen. Preverite, ali ste pri odčitavanju lege vedno opazovali isto točko na kroglici. Poskusite ponovno.
Primerjava rezultatov
S pomočjo slik ste izmerili hitrost kroglice ( m/s), izračunali pa ste hitrost ( m/s). Z besedami pojasnite, kaj lahko sklepamo na podlagi ujemanja izmerjene in izračunane vrednosti.
Uspešno ste končali z glavnim delom naloge. Ali ste pripravljeni odgovoriti še na nekaj vprašanj, povezanih z vodoravnim metom?
Končali ste z reševanjem nalog.
Žogica v luknji
- Da kroglica zanesljivo pade v luknjo, se mora spustiti za polmer. Izračunajte čas, v katerem se to zgodi. Za polmer kroglice vzemite cm.
- s
Odlično! Lahko nadaljujemo.
Rezultat je žal napačen. Pravilen odgovor je s. Nadaljujte z nalogo.
Rezultat je napačen. Preverite, ali ste upoštevali, da je padanje enakomerno pospešeno gibanje.
Hitrost kroglice
- Izračunajte hitrost kroglice. Širina luknje je cm.
- m/s
Odgovor je pravilen.
Odgovor je napačen. Pravilen rezultat je m/s m/s. Nadaljujte z nalogo.
Odgovor ni pravilen. Pomagajte si z namigom.
- V času, ki ste ga izračunali, se kroglica premakne do stene luknje. S skice določite pot, ki jo kroglica prepotuje v vodoravni smeri, nato pa izračunajte hitrost kroglice v vodoravni smeri. Širina luknje je cm, premer kroglice pa cm.
Hitrost v navpični smeri
- Izračunajte komponento hitrosti, ki jo ima kroglica v navpični smeri ob času s po začetku padanja v luknjo. Za g vzemite m/s2.
m/s
Odlično, lahko nadaljujemo.
Odgovor je napačen. Pravilen odgovor je m/s. Svetujemo vam, da si v učbeniku preberete poglavje o prostem padu.
Odgovor je napačen. Gibanje v navpični smeri je enakomerno pospešeno. Preverite, ali ste uporabili pravilno enačbo.
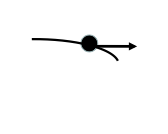
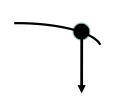
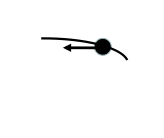
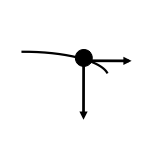
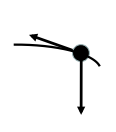
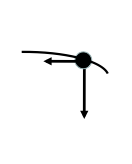
Smer vektorja hitrosti
- Slika prikazuje tirnico, po kateri se je gibala kroglica. V katerem primeru je pravilno prikazan vektor hitrosti kroglice ob času 0.05 s?
- Učenci naj bi vedeli, da vektor hitrosti v neki točki kaže tangentno na tirnico. Pričakujemo, da bodo izbirali odgovore, ki prikazujejo samo eno komponento vektorja hitrosti.
Odlično! Odgovor je pravilen.
Odgovor ni pravilen. Preverite, ali ste upoštevali, da je vektor hitrosti kroglice sestavljen iz vodoravne in navpične komponente hitrosti.
Hitrost po nekaj časa
- Izračunaj, kolikšna je hitrost kroglice ob času s po začetku vodoravnega meta.
m/s
Kar tako naprej!
Odgovor ni pravilen. Uporabite Pitagorov izrek.
Odgovor je napačen. Pravilen odgovor je m/s.
Za vodoravno komponento hitrosti vzemi m/s.
Sile na kroglico
- Slika prikazuje tirnico, po kateri se je gibala kroglica. Katera slika pravilno prikazuje sile, ki delujejo na kroglico med padanjem? Zračni upor zanemari.
- Če zračni upor zanemarimo, deluje na telo le sila teže. Pričakujemo, da bodo odgovarjali enako/podobno kot na vprašanje o vektorju hitrosti.
Odlično, lahko nadaljujemo.
Odgovor ni pravilen. Poskusite ponovno.
Sile z upoštevanim zračnim uporom
- Katera slika pravilno prikazuje sile, ki delujejo na kroglico med padanjem, če zračnega upora ne zanemarimo?
- Če zračnega upora ne zanemarimo, deluje na telo sila teže in sila upora, ki kaže v nasprotni smeri od gibanja telesa. Pravilen odgovor je torej (c).
Odlično! Lahko nadaljujemo.
Odgovor ni pravilen. Razmislite, kam kaže sila upora.
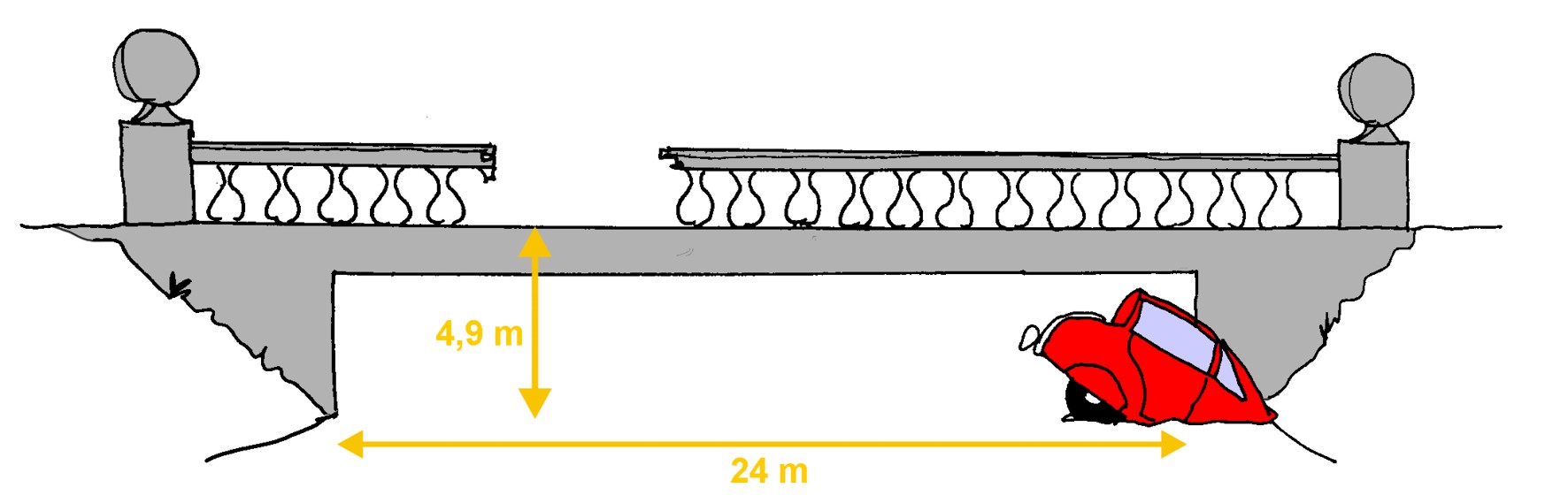
Na mostu
Ali je voznik avtomobila vozil prehitro? Omejitev na mostu je m/s, ostale podatke razberite s slike.
|
Odlično! Končali ste z nalogo.
Odgovor žal ni pravilen. Končali ste z nalogo.
Za radovedne
O filmu Hitrost (Speed)
V filmu Speed, s Keanu Reevesom in Sandro Bullock v glavnih vlogah, avtobus vozi s hitrostjo približno 80 km/h in preskoči večmetrsko luknjo v cesti. Cesta iz filma je videti vodoravna, brez naklona. Bi imela igralca v resnici kaj možnosti za uspešen preskok luknje?
