Integrali - teorija (druga različica)

Integrali - teorija (druga različica)

Avtor: Skupina NAUK

Več o projektu...

Nedoločeni integral

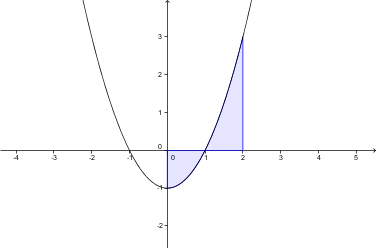
Ko odvajamo funkcijo dobimo . Vprašajmo se obratno: poznamo odvod , katero funkcijo moramo odvajati, da dobimo ta odvod.

To z znaki napišemo takole oziroma splošno in preberemo "nedoločeni integral funkcije ".

Nedoločeni integral funkcije je taka funkcija , da velja . Postopek imenujemo integriranje. Integriranje je obratna operacija od odvajanja.

 
, tako da



Poglejmo, odvod katere funkcije je . To je lahko , lahko je samo , lahko pa je tudi npr. ...

Možnih je torej več rešitev , vse pa se razlikujejo samo za konstanto. Zato nedoločeni integral zapišemo kot

 
, je konstanta.

PREMISLITE

Koliko rešitev ima nedoločeni integral funkcije?

Odgovor

Kaj grafično predstavlja ?

Odgovor

Zakaj rečemo nedoločeni integral?

Odgovor

Nedoločeni integral ima neskončno rešitev. Vse rešitve se razlikujejo za konstanto.

Zgled: Podan imamo odvod in iščemo izvorno funkcijo.
dobimo, če odvajamo , dobimo pa tudi, če odvajamo , , ...
Vse te rešitve imajo skupen del in različno konstanto. Ker je različnih konstant neskončno, je tudi rešitev nedoločenega integrala neskončno.

C predstavlja premik funkcije po osi. Oblika funkcije ostane ista.

Aplikacija GeoGebra se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Geogebra datoteka

Nedoločeni integral je zato, ker vrednosti C ne poznamo. Konstanta C ni določena, zato tudi integral ni določen.

Tabela nedoločenih integralov

PREMISLITE

Kako dokažemo formule iz tabele?

Odgovor

Da formule držijo pokažemo na preprost način. Vzamemo desno stran enačbe in jo odvajamo. Če dobimo enako funkcijo, kot je na levi strani, potem enačba velja.

Zgled:

Pokažimo, da velja .

Vzamemo desno stran in jo odvajamo:



Dobili smo funkcijo z leve strani.

Pravila za integriranje

  1. Integriranje vsote:

    Enako pravilo velja za integriranje razlike.

  2. Integriranje produkta funkcije s konstanto:

Zgled:

Izračunajmo nedoločeni integral funkcije .






Zgled

PREMISLITE

Kdaj napišemo v račun?

Odgovor

v račun napišemo samo na koncu, ko ni nobenega integrala več. Poglejmo zakaj:




lahko združimo v eno konstanto, zato pišemo vedno samo , ne glede na to, koliko integralov imamo v vsoti.

Določeni integral

Določeni integral označimo kot , je spodnja meja in je zgornja meja določenega integrala. Vrednost izraza je enaka ploščini lika med grafom funkcije f(x) in abscisno osjo na intervalu .

(integral_doloceni.png)



Slika prikazuje .

PREMISLITE

Od kod izhaja oznaka za integral in kakšna je njena povezava z določenim integralom?

Odgovor

Oznaka za integral izhaja iz črke kot oznake za vsoto (suma).

pomeni vsoto ploščin pravokotnikov z zelo majhno širino in višino f(x). Manjši kot je , bolj natančno vsota ploščin pravokotnikov opiše ploščino lika pod krivuljo .

Aplikacija GeoGebra se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Geogebra datoteka

Zveza med določenim in nedoločenim integralom

Izračunati znamo nedoločeni integral in vemo, da določeni integral pomeni ploščino lika med krivuljo in abscisno osjo. S pomočjo nedoločenega integrala lahko izračunamo določeni integral in tako natančno izračunamo ploščino.

Nedoločeni integral je .

 

Formula za računanje določenega integrala:

To zvezo med določenim in nedoločenim integralom imenujemo Newton-Leibnizova formula ali osnovni izrek integralskega računa.

Zgled:

Izračunajmo določeni integral :







Zgled

PREMISLITE

Kam pri računanju določenega integrala izgine konstanta ?

Odgovor

Vidimo, da se odšteje.

Lastnosti določenega integrala

  1. Vseeno je, kako poimenujemo spremenljivko: .

  2. Če zamenjamo spodnjo in zgornjo mejo, se spremeni predznak integrala:

  3. Če sta spodnja in zgornja meja enaki, je vrednost integrala nič:

  4. Če je točka med in , potem velja:

    (integral_d_vsota.png)

Določeni integral in ploščina

Vrednost določenega integrala je enaka vrednosti ploščine lika, ki ga oklepata graf pozitivne funkcije in os med mejama določenega integrala.

Če je funkcija na integracijskem intervalu negativna, je vrednost integrala negativna.

(integral_d_negativen.png)

Ploščina je vedno pozitivno število zato je, kadar je funkcija negativna, ploščina enaka:

Ploščina lika med krivuljo in abscisno osjo

S pomočjo določenega integrala lahko izračunamo ploščino lika med krivuljo in abscisno osjo. Pri tem nam pomagajo lastnosti določenega integrala. Pri računanju si pomagamo s sliko.

Imamo funkcijo . Izračunajmo ploščino osenčenega dela, to je na intervalu .

(integral_ploscina.png)

Izračunati moramo Integral razdelimo na vsoto dveh integralov, tako kot je ploščina na sliki razdeljena na dva dela. Za novo mejo, ki jo potrebujemo, vzamemo ustrezno ničlo funkcije. Ničle Hkrati upoštevamo še, da je integral negativen tam, kjer je osenčeni del pod abscisno osjo. Dobimo:

Zdaj pa samo še izračunamo vrednost integrala po pravilih za računanje integralov.

Izračun

Določimo ničle funkcije:

Ničle so:






Ploščina lika med dvema krivuljama

(integral_ploscina2_1.png) (integral_ploscina2_2.png) (integral_ploscina2.png)

Ploščina lika med grafom funkcije f in abscisno osjo je (prva slika).
Ploščina lika med grafom funkcije g in abscisno osjo je (druga slika).

Ploščina lika med obema krivuljama (tretja slika) je ravno razlika obeh ploščin , to še drugače zapišemo kot

Meji integrala sta koordinati presečišč obeh krivulj. Vedno odštevamo spodnjo funkcijo od zgornje, zato si pri računanju pomagamo s sliko.

Zgled

PREMISLITE

Kako izračunamo ploščino, če lik ni v celoti nad abscisno osjo?

Odgovor

Kadar lik ni v celoti nad osjo, ga lahko premaknemo tako, da bo. To storimo tako, da funkcijama in prištejemo neko dovolj veliko število .

Aplikacija GeoGebra se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Poglejmo, kaj se zgodi s formulo za izračun ploščine:

Število se odšteje in dobimo enako formulo kot prej. Torej, ne glede na to, kje v koordinatni ravnini leži lik, računamo njegovo ploščino na enak način, po formuli

Geogebra datoteka

Določite ploščino lika med krivuljama in .

Najprej določimo presečišči (oziroma dovolj je koordinati presečišč):





Iz slike razberemo, katera funkcija je zgoraj in katera spodaj: je zgoraj, je spodaj.

Napišemo enačbo za ploščino in izračunamo:






0%
0%