Funkcija (preslikava, transformacija) je predpis, ki vsakemu elementu iz množice priredi natanko en element iz množice . Elementi množice sestavljajo definicijsko območje funkcije . Množico njihovih slik pa imenujemo zaloga vrednosti funkcije . Množica lahko vsebuje tudi elemente, ki niso slike nobenega elementa množice .
Če sta množici in množici realnih števil , imenujemo funkcijo realna funkcija realne spremenljivke.
Funkcije - teorija
Funkcije - teorija
Skupina NAUK
Razumevanje pojmov funkcija, definicijsko območje in zaloga vrednosti funkcije, opis lastnosti realnih funkcij, graf inverzne funkcije, transformacije v ravnini ter spoznavanje limite funkcije.
Definicija funkcije
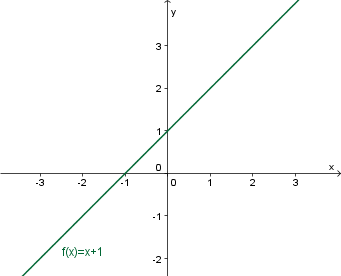
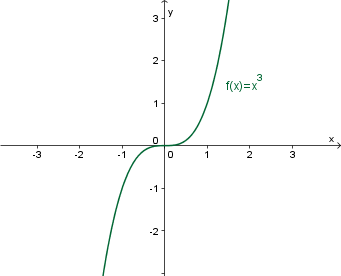
Definicijsko območje funkcije so vsa realna števila , prav tako je zaloga vrednosti .
Graf funkcije
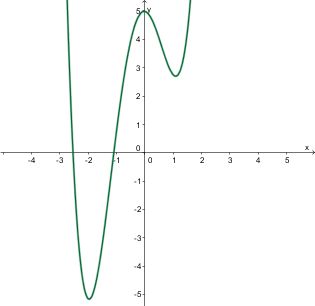
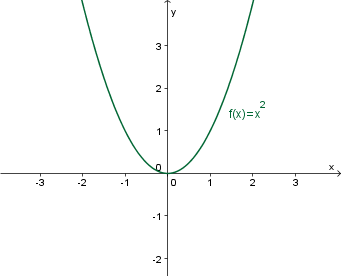
Graf funkcije je množica vseh urejenih parov , kjer je in . Urejene pare lahko narišemo v koordinatnem sistemu, kjer vsakemu paru v koordinatnem sistemu pripada točka, katere abscisa je , ordinata pa njegova slika .
Zgled: Narišite graf funkcije .
Rešitev:
Napišemo nekaj urejenih parov:
| x | f(x)=x+1 |
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
in narišemo graf.
Premiki in raztegi grafov funkcij
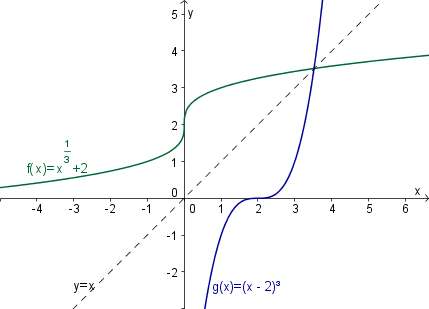
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije togo premaknemo za vzdolž ordinatne osi navzgor () oz. navzdol ().
Premiki in raztegi grafov funkcij
Naj bo funkcija definirana kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije togo premaknemo za vzdolž abscisne osi v desno () oz. levo ().
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije :
- skrčimo za faktor vzdolž ordinatne osi, če je ,
- raztegnemo za faktor vzdolž ordinatne osi, če je ,
- zrcalimo čez abscisno os in skrčimo za vzdolž ordinatne osi, če je ,
- zrcalimo čez abscisno os in raztegnemo za vzdolž ordinatne osi, če je .
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot , kjer je .
Graf funkcije dobimo tako, da graf funkcije raztegnemo oziroma skrčimo vzdolž abscisne osi. Funkcija doseže enako vrednost kot funkcija pri -krat manjši abscisi .
Premiki in raztegi grafov funkcij
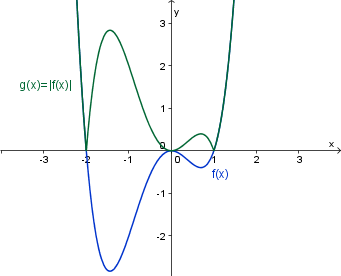
Definirajmo funkcijo kot .
Graf funkcije dobimo tako, da vse točke grafa funkcije , ki imajo negativno ordinato , prezrcalimo čez abscisno os.
Premiki in raztegi grafov funkcij
Definirajmo funkcijo kot .
Graf funkcije dobimo tako, da najprej narišemo za pozitivne () graf funkcije , nato pa ga prezrcalimo čez ordinatno os, saj velja .
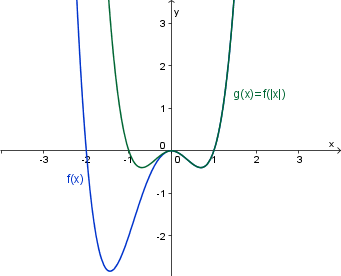
Zaloga vrednosti funkcije, ki je podana z absolutno vrednostjo, je večja ali enaka 0:
Lastnosti realnih funkcij
Injektivnost:
Funkcija je injektivna, če je vsak element iz zaloge vrednosti slika natanko enega elementa iz .
Surjektivnost:
Funkcija je surjektivna, če je vsak element iz množice slika vsaj enega elementa iz množice ().
Bijektivnost:
Funkcija je bijektivna, če je injektivna in surjektivna hkrati.
Naraščanje, padanje, omejenost
Funkcija je na intervalu naraščajoča, če za poljubna in s tega intervala velja: .
Funkcija je na intervalu padajoča, če za poljubna in s tega intervala velja: .
Funkcija je navzdol omejena, če obstaja tako realno število , da je za vsak .
Funkcija je navzgor omejena, če obstaja tako realno število , da je za vsak .
Funkcija je omejena, če je navzgor in navzdol omejena.
Zgled: Proučite lastnosti funkcije na sliki.
Rešitev:
Definicijsko območje funkcije so vsa realna števila, zaloga vrednosti . Funkcija ni injektivna in ni surjektivna, torej ni bijektivna. Naraščajoča je na intervalih () in (), padajoča pa na intervalih () in (). Funkcija je navzdol omejena.
Sodost in lihost funkcije
Funkcija je soda, če za vsak velja:
Graf sode funkcije je simetričen glede na ordinatno os.
Funkcija je liha, če za vsak velja:
Graf lihe funkcije je simetričen glede na koordinatno izhodišče.
|
|
Ničle funkcije
Število imenujemo ničla funkcije natanko takrat, ko velja . Funkcija ima torej v ničli vrednost .
Graf funkcije v ničlah seka abscisno os ali pa se je le dotika.
Ničle funkcije poiščemo tako, da rešimo enačbo .
Inverzna funkcija
Če je funkcija bijektivna, potem obstaja inverzna funkcija , tako da velja:
Inverzno funkcijo dane funkcije poiščemo tako, da v funkcijskem predpisu med seboj zamenjamo odvisno () in neodvisno () spremenljivko. Graf inverzne funkcije narišemo tako, da dano funkcijo zrcalimo preko simetrale lihih kvadrantov.
Zgled:Dana je funkcija . Nariši graf dane funkcije in njene inverzne funkcije.
Rešitev:
Najprej narišemo graf funkcije .
Zapišemo inverzno funkcijo ter izrazimo . Dobimo: in narišemo graf.
Računske operacije s funkcijami
Vzemimo realni funkciji . Med njima lahko izvajamo naslednje računske operacije:
- Vsota in razlika funkcij:
- Produkt funkcij:
- Kvocient funkcij: , kjer
- Produkt funkcije s številom:
- Kompozitum funkcij: Vzemimo funkciji in . Kompozitum je funkcija podana s predpisom oziroma .
Limita funkcije
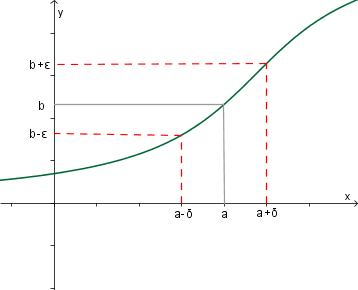
Limita funkcije v točki je število, ki se mu vrednost funkcije približuje, ko se vrednost spremenljivke približuje danemu številu . Torej limita funkcije v točki je , če za vsak obstaja tak , da iz () sledi .
Pravila za računanje limite
1.
2.
3.
4. , kjer
Limita v neskončnosti in neskončna limita
Limita v neskončnosti: , če za vsak obstaja tak , da za velja . V tem primeru je premica vodoravna asimptota grafa funkcije .
Neskončna limita: , če za vsak obstaja tak , da iz () sledi . V tem primeru ima graf funkcije v točki navpično asimptoto.
- Definicija funkcije
- Graf funkcije
- Premiki in raztegi grafov funkcij
- Lastnosti realnih funkcij
- Naraščanje, padanje, omejenost
- Sodost in lihost funkcije
- Ničle funkcije
- Inverzna funkcija
- Računske operacije s funkcijami
- Limita funkcije
- Pravila za računanje limite
- Limita v neskončnosti in neskončna limita
