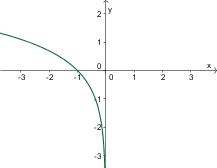
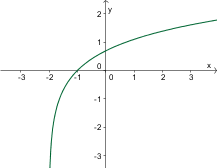
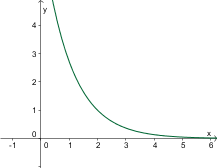
Kateri izmed danih grafov predstavlja graf funkcije ?
Logaritemska funkcija - vaje
Logaritemska funkcija - vaje
Skupina NAUK
Urjenje logaritemske funkcije.
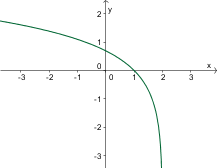
Graf logaritemske funkcije
Napačno
Odgovor je napačen.
Najprej narišemo graf eksponentne funkcije . Nato graf zrcalimo preko simetrale . Dobimo graf logaritemske funkcije .
Logaritemske enačbe
Rešite enačbo .
Napačno
Odgovor je napačen.
Pri reševanju logaritemskih enačb si pomagamo s pravilom .
Torej enačbo prevedemo na enačbo .
Dobimo rešitev .
Logaritemske enačbe
Rešite enačbo .
Logaritmiranje izrazov
Logaritmirajte izraz .
Logaritemske enačbe
Iz enačbe izrazite .
Logaritemske enačbe
Rešite enačbo: .
Napačno
Odgovor je napačen.
Rešitev dobimo z upoštevanjem pravila za reševanje logaritemskih enačb . V tem primeru
imamo logaritem z osnovo . Torej lahko enačbo prevedemo na . Za rešitev te linearne
enačbe dobimo .
Logaritemske enačbe
Rešite enačbo .
Napačno
Odgovor je napačen.
Pri reševanju enačbe najprej uporabimo pravilo (kjer sta ), in prevedemo enačbo na .
Tu upoštevamo pravilo za reševanje logaritemskih enačb in dobimo:
Rešimo linearno enačbo in dobimo rešitev .
Rezultati
