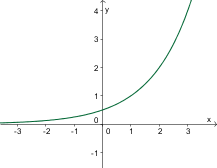
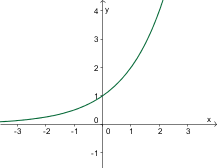
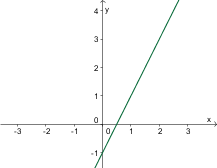
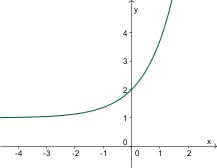
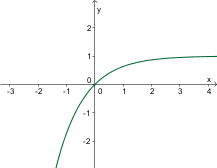
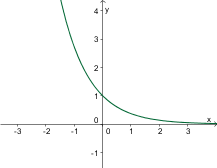
Izmed danih grafov izberite graf funkcije .
Eksponentna funkcija - vaje
Eksponentna funkcija - vaje
Skupina NAUK
Urjenje eksponentne funkcije.
Graf eksponentne funkcije
Napačno
Odgovor je napačen.
Asimptota grafa funkcije je . Pravilen graf je torej eksponentna funkcija premaknjena po ordinatni osi za .
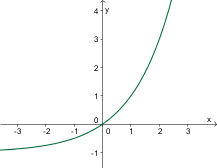
Presečišči eksponentne funkcije s koordinatnima osema
Dana je funkcija . Poiščite presečišči funkcije s koordinatnima osema.
Napačno
Odgovor je napačen.
Presečišča funkcije s koordinatnima osema izračunamo po naslednjem postopku:
| : | : | |||
Dobimo presečišči in .
Eksponentna funkcija z osnovo e
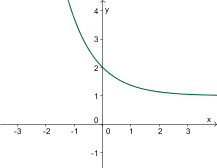
Izmed danih grafov izberite graf funkcije .
Napačno
Odgovor je napačen.
Graf funkcije narišemo tako, da graf premaknemo za po ordinatni osi. Asimptota grafa
funkcije je .
Eksponentne enačbe
Izberite pravilno rešitev enačbe .
Napačno
Odgovor je napačen.
Najprej prevedemo vse člene enačbe na isto osnovo:
Izenačimo eksponente:
Rešitev enačbe je:
Eksponentne enačbe
Rešite enačbo . Izmed danih rešitev izberite pravilno.
Napačno
Odgovor je napačen.
Upoštevamo lastnost računanja s potencami, da je za . Torej je . Eksponent mora biti torej enak .
Izenačimo: .
Razstavimo: .
Enačba ima dve rešitvi: in .
Lokvanj in ribnik
Biologi so odkrili novo vrsto lokvanja, ki se razmnožuje zelo hitro. Prvi dan so v ribnik posadili eno rastlino, naslednji dan sta bili že dve. Ugotovili so, da se število lokvanjev vsak dan podvoji. Danes je deseti dan in z lokvanji je prekrita že polovica ribnika. Kdaj bo ribnik v celoti prekrit z lokvanji?
Napačno
Odgovor je napačen.
Če se vsak dan število lokvanjev podvoji, potem imamo eksponentno rast. Prvi dan imamo lokvanj, naslednji dan lokvanja, tretji dan itd. Deseti dan imamo torej lokvanjev. Naslednji dan bomo imeli lokvanjev, kar pomeni, da bo ribnik popolnoma prekrit.
Rezultati
