Okolica števila
Točka v koordinatnem sistemu ima dve koordinati,
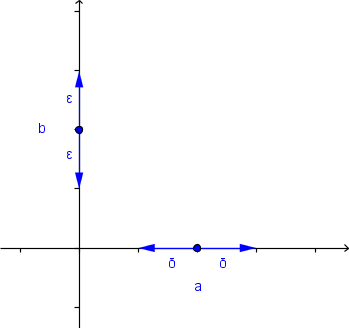
Okolica točke
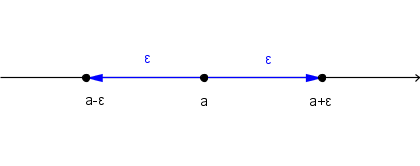
Okolica števila

Točka v koordinatnem sistemu ima dve koordinati,

Limita funkcije
Limita funkcije je število, proti kateremu gredo funkcijske vrednosti, če gredo vrednosti neodvisne spremenljivke proti
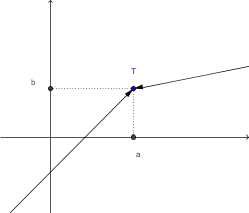
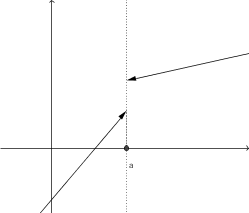
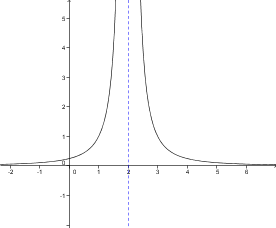
Na levi sliki vidimo, da ko se vrednosti
Formalna definicija limite
Če za vsak
Z znaki to napišemo takole:
Če vzamemo
Pravila za računanje limit
Za računanje limite funkcije veljajo enaka pravila kot za računanje limite zaporedja:
Seznam najpogostejših limit
Računanje limit
Limite računamo na naslednji način:
Najprej v limito vstavimo namesto
Števec in imenovalec razstavimo in okrajšamo. Potem spet vstavimo vrednost v limito.
Če nastopa v ulomku koren v razliki, potem racionaliziramo. Potem zopet poskusimo z vstavljanjem vrednosti.
Imamo limito, ko gre
Enako velja za katerikoli drug izraz, s katerim želimo krajšati ulomek pri računanju limit.
Limite kotnih funkcij
Kadar računamo limite kotnih funkcij, si pomagamo z naslednjim pravilom:
Zgled 1:
Zgled 2:
Neskončna limita
Do zdaj smo obravnavali dve možnosti, ki ju dobimo pri računanju limite, definirano vrednost in
Poglejmo
Če ima izraz, katerega limito iščemo, negativen predznak, potem je limita tega izraza
Limita v neskončnosti
Do zdaj smo gledali limite, ko gre
Pglejmo limito
Limita funkcije v neskončnosti je podobna limiti zaporedja, samo da smo pri zaporedjih gledali samo vrednosti naravnih števil
Limito v neskončnosti računamo na enak način kot limito zaporedja. Veljajo enaka pravila in postopki računanja:
Asimptote funkcij
Limita grafično predstavlja premico. Kadar imamo neskončno limito, je to navpična premica. Graf funkcije se premici približuje, ko
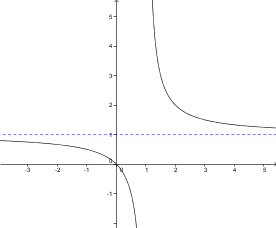
Kadar govorimo o limiti v neskončnosti, je premica vodoravna. Graf funkcije se premici približuje, ko