Naklonski kot
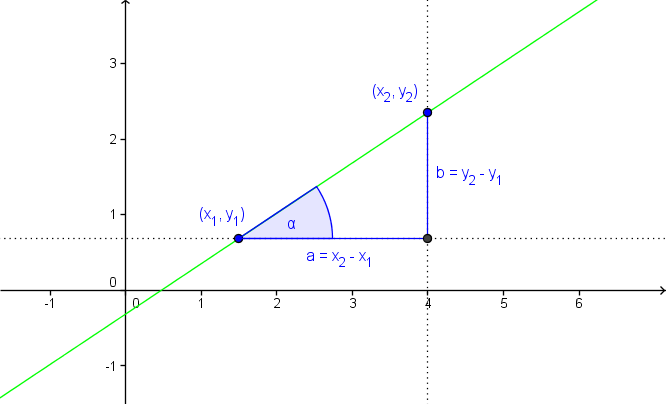
Naklonski kot
Pri premici je strmina enaka za celo premico, zato je vseeno, kateri dve točki na premici vzamemo, da izračunamo
Naklonski kot in smerni koeficient premice
Naklonski kot

Naklonski kot
Pri premici je strmina enaka za celo premico, zato je vseeno, kateri dve točki na premici vzamemo, da izračunamo
Diferenčni količnik
Kadar imamo krivuljo, ki ni premica, naklonskega kota in smernega koeficienta ne moremo izračunati za celo krivuljo. Lahko pa izračunamo naklonski kot in smerni koeficient premice, ki poteka skozi dve bližnji točki na krivulji. Izberemo si števili
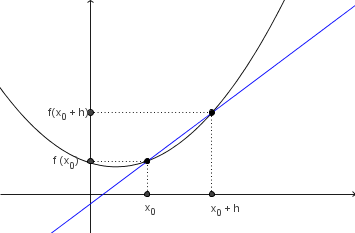
Izrazu
Če je
Odvod
Če
Geogebra datoteka
Če ta limita obstaja, jo označimo z
Geometrijski pomen odvoda
Vemo že, da diferenčni količnik predstavlja naklon premice med dvema točkama oziroma približen naklon funkcije med tema dvema točkama. Ko
Vrednost odvoda funkcije v dani točki je torej enaka smernemu koeficientu tangente na krivuljo v dani točki. To pomeni, da odvod funkcije pove, kakšen je naklon krivulje v dani točki.
Ker je odvod
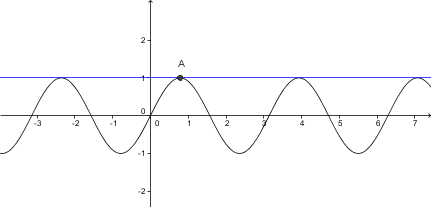
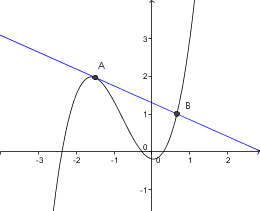
Tangenta je premica, ki se krivulji najbolj prilega v okolici dane točke. To pomeni, da stran od te točke krivuljo lahko seka ali pa se lahko krivulje dotika še v kateri drugi točki. Poglejte dva primera:
Odvajanje funkcij po definiciji
Vzemimo funkcijo
| Definicija odvoda: | |
| Namesto f(x) in f(x+h) vstavimo dano funkcijo: | |
| Izračunamo števec ulomka: | |
| Odštejemo in delimo s h: | |
| Izračunamo limito (vstavimo h=0 v izraz): |
Dobili smo rezultat, odvod funkcije
Odvodi elementarnih funkcij
Po definiciji lahko izračunamo odvode vseh funkcij, vendar si za hitrejše računanje kar zapomnimo odvode elementarnih funkcij.
|
| |||||||||||||||||||||||||||
|
|
Pravila za odvajanje
Na voljo imamo tudi nekaj pravil za odvajanje, kadar želimo odvajati bolj kompleksne funkcije.
1. ODVOD VSOTE IN RAZLIKE DVEH FUNKCIJ | Zgled: |
2. ODVOD PRODUKTA KONSTANTE IN FUNKCIJE | Zgled: |
3. ODVOD PRODUKTA DVEH FUNKCIJ | Zgled: |
4. ODVOD KOLIČNIKA DVEH FUNKCIJ | Zgled: |
5. ODVOD SESTAVLJENE FUNKCIJE | Zgled: |
Zgledi uporabe pravil za odvajanje
1.
2.
3.
Rešitev
Uporaba odvoda - tangenta in normala
Grafični pomen odvoda je naklon premice tangente v dani točki. To pomeni, da lahko s pomočjo odvoda izračunamo enačbo tangente v dani točki.
Zgled:
Dana je krivulja
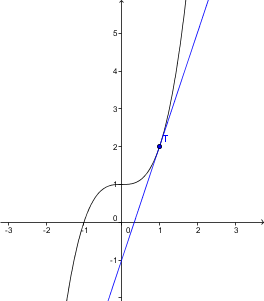
Če poznamo naklon tangente, lahko izračunamo tudi enačbo premice normale skozi dano točko na krivulji. Normala na krivuljo skozi dano točko je pravokotnica na tangento skozi to točko. Smerni koeficient
Kot med krivuljama je kot med tangentama na krivulji v njunem presečišču. Točka
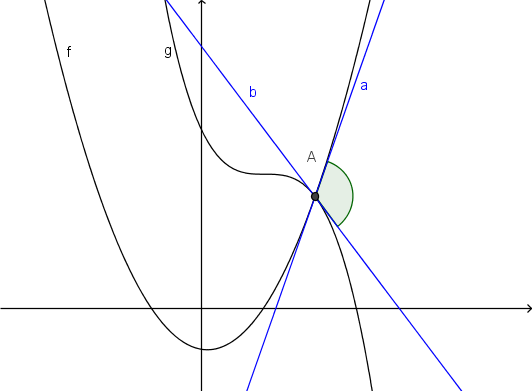
Najprej izračunamo presečišče krivulj. Potem izračunamo odvoda obeh krivulj in vrednosti odvoda v presečišču, da dobimo koeficienta obeh tangent. Nazadnje uporabimo formulo
Obstajata dva kota med krivuljama. Zaradi absolutne vrednosti nam formula da tangens ostrega kota, vendar lahko enostavno izračunamo tudi drugi kot, saj je njuna vsota
Poiščimo kot med krivuljama
Naraščanje in padanje
Iz grafa funkcije lahko razberemo naraščanje in padanje funkcije.
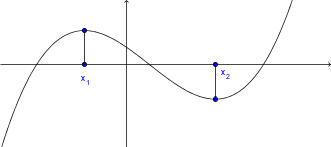
Funkcija narašča za
Če pa grafa funkcije ne poznamo, lahko naraščanje in padanje funkcije ugotovimo z odvodom.
Stacionarne točke
Stacionarne točke so točke na krivulji, v katerih je odvod funkcije enak nič
To pomeni, da je smerni koeficient tangente enak 0, kar pomeni, da je tangenta v taki točki vzporedna z osjo
Na sliki poglejmo, kakšne so možne stacionarne točke.
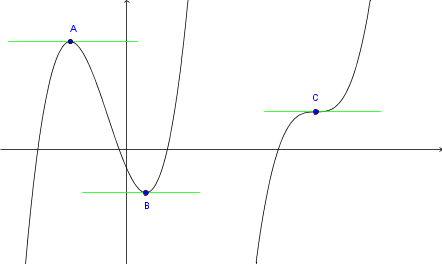
Stacionarne točke funkcije določimo tako, da najprej izračunamo odvod funkcije, potem pa ta odvod izenačimo z
Ekstremi
Največje (maksimum) in najmanjše (minimum) vrednosti funkcije s skupno besedo imenujemo ekstremi funkcije. Grafično jih prepoznamo kot "vrhove" in "doline" na grafu, formalno pa ekstreme definiramo takole:
Funkcija ima lahko več lokalnih maksimumov in minimumov ampak samo en globalni maksimum in en globalni minimum. Ta dva definiramo takole:
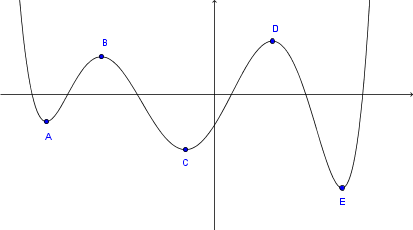
Točke
Zakaj točka D ni globalni maksimum?
Ekstremi med stacionarnimi točkami
Poglejmo, kako računsko določimo minimume in maksimume med stacionarnimi točkami.

| 
| 
|
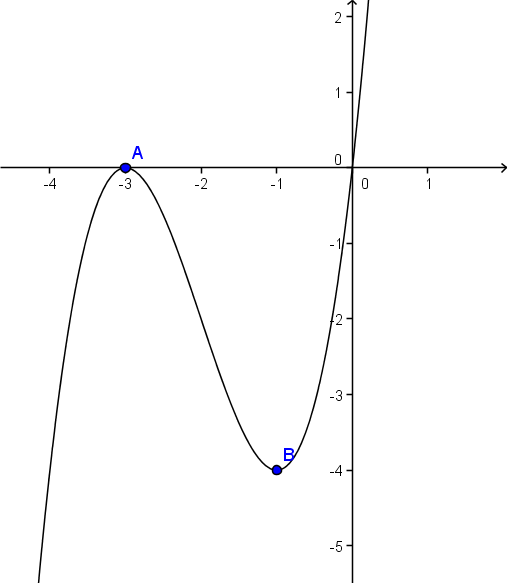
V točki A je minimum. Levo od točke A funkcija pada, desno pa narašča. Z odvodom to definiramo takole:
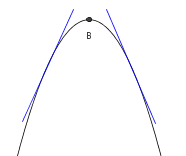
V točki B je maksimum. Levo od točke B funkcija narašča, desno pa pada:
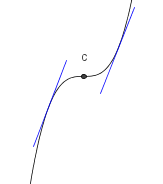
V točki C ni ne minimum ne maksimum. Levo in desno od točke C funkcija narašča:
Ekstreme funkcije določimo tako, da najprej poiščemo stacionarne točke, potem pa določimo predznak odvoda med stacionarnimi točkami.
Določimo stacionarne točke:
Določimo predznak odvoda (v enačbo odvoda vstavimo eno izmed vrednosti na intervalu, za katerega določamo predznak):
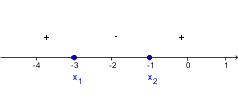
V
Ni nujno, da je kateri od lokalnih ekstremov tudi globalni ekstrem. Zgled:

Levo in desno od označenih točk vrednosti funkcije rastejo v neskončnost. V točki D, ki je sicer največji od lokalnih maksimumov, torej ni največja vrednost funkcije na celotnem definicijskem območju, zato točka D ni globalni maksimum.
Ekstremalni problemi
Računanje ekstremov nam prav pride v praksi.
Zgled:
Radi bi zgradili leseno hišo s prostornino
Nalogo rešimo tako, da tisto količino, ki naj bo največja ali najmanjša, proglasimo za funkcijo, potem izračunamo odvod te funkcije, ga izenačimo z 0 in določimo ekstreme. Med ekstremi potem poiščemo tistega, ki ga iščemo.
Rešitev zgleda:
Količina, ki naj bo najmanjša, je površina sten. Napišemo enačbo za izračun:
Ker imamo v enačbi dve neznanki, v funkciji pa želimo samo eno, eno izrazimo z drugo s pomočjo enačbe za volumen.
In odvod izenačimo z 0, da dobimo stacionarne točke:
Lahko se še prepričamo, da smo res dobili minimum:
PREMISLITE
V enačbo za površino vstavite za dolžino in širino drugačne številke in se prepričajte, da je izračunana res najboljša.
Enačba za površino je
Iz enačbe za volumen smo dobili naslednjo enačbo:
Obe izračunani površini sta večji od površine, izračunane s pomočjo odvoda in ekstremov.
Sami lahko poskusite še druge dolžine sten