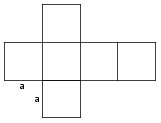
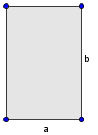
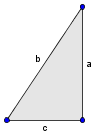
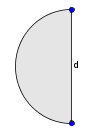
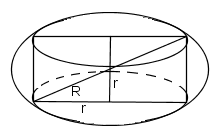
Povlecite obrazce k pravim slikam.
Geometrijska telesa - vaje
Telesa
Pokončna tristrana prizma
Pokončna tristrana prizma ima prostornino . Osnovna ploskev prizme je enakokraki trikotnik s krakoma in osnovnico . Koliko meri njena površina?
Napačno
Odgovor je napačen. Skica prizme:
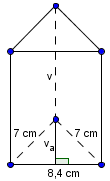
| Izračun višine na osnovnico | Izračun ploščine osnovne ploskve | Prostornina ali volumen | Izračun površine |
| | | | |
Površina prizme je .
Volumen bazena
Bazen dolžine 16 m, širine 4 m in višine 1,5 m bi radi napolnili z vodo. Koliko litrov vode potrebujemo, da ga napolnimo?
Napačno
Odgovor je napačen. Bazen je v obliki kvadra in ker naloga sprašuje, koliko litrov potrebujemo, da ga napolnimo, je potrebno izračunati prostornino ali volumen bazena.
Ker pa naloga zahteva rezultat v litrih, ga moramo pretvoriti. Ker je in , je in zato litrov.
Prizma, kocka in kvader
V okenca vpišite pravilne odgovore na zastavljena vprašanja.
Koliko robov ima kocka?
Koliko mejnih ploskev ima kvader?
Koliko oglišč ima petstrana prizma?
Koliko osnovnih ploskev ima prizma?
Napačno
Odgovor je napačen. Če preštejemo vse robove kocke, naštejemo dvakrat po 4 robove na osnovnih ploskvah in še štiri stranske robove, skupaj torej 12 robov. Kvader ima 2 osnovni ploskvi in 4 stranske, skupaj 6 mejnih ploskev. Petstrana prizma ima za osnovno ploskev petkotnik, ki ima 5 oglišč, ker pa ima prizma 2 osnovni ploskvi, ima petstrana prizma skupaj 10 oglišč.
Pravilni odgovori bi bili po vrsti , , , .
Valj
Ploščina osnega preseka enakostraničnega valja je . Koliko blaga potrebujemo, da ovijemo ta valj?
Napačno
Odgovor je napačen. Ker je valj enakostraničen, lahko izračunamo polmer tega valja:
Potrebno je izračunati površino valja, da bi izvedeli, koliko blaga potrebujemo, da ovijemo valj:
Rezultat je v enoti , zato ga pretvorimo v željeno enoto, v . Ker je , je . Pravilen odgovor je, da za ovoj valja potrebujemo blaga.
Valj
Plašč valja s polmerom osnovne ploskve meri , kolikšna je prostornina valja?
Napačno
Odgovor je napačen. Plašč valja je pravokotnik s stranicama in , kjer je obseg kroga, osnovne ploskve valja in višina valja. Prostornina pa se izračuna z obrazcem . Iz podatkov lahko izrazimo višino in izračunamo prostornino:
Vrtenje okoli osi
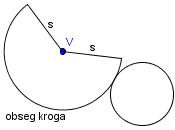
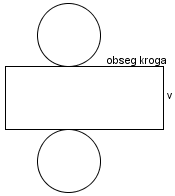
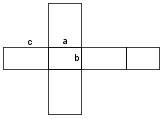
Kaj dobimo, če zavrtimo za polni kot okoli ene stranice:
Napačno
Odgovori so napačni. Če zavrtimo pravokotnik okoli stranice, dobimo valj. Če zavrtimo pravokotni trikotnik okoli stranice, dobimo stožec, in če zavrtimo polkrog okoli premera, dobimo kroglo.
Piramida
Podan je pravilni tetraeder.
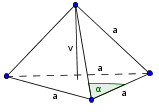
Koliko meri kot med stransko in osnovno ploskvijo?
Osnovni rob tetraedra meri . Koliko meri površina tetraedra, če jo zaokrožite na celo število? cm
Ploščina osnovne ploskve tetraedra meri , njegova višina pa . Koliko meri prostornina tetraedra?
Napačno
Odgovori niso pravilni.
Kot med stransko in osnovno ploskvijo je kot v trikotniku stranske ploskve. Ker gre za enakostranični trikotnik, lahko brez računanja ugotovimo, da je kot .
Obrazec za površino tetraedra je izpeljan v gradivu Geometrijska telesa - teorija in je . Podan je osnovni rob, , zato lahko izračunamo površino: . Ker pa naloga zahteva rezultat, zaokrožen na celo število, je to .
Prostornina katerekoli piramide je . Podano imamo ploščino osnovne ploskve in višino, zato je prostornina tetraedra .
Pravilna 4-strana piramida
Pri pravilni 4-strani piramidi s površino sta osnovni rob in višina v razmerju . Koliko meri osnovni rob piramide?
Napačno
Odgovor je napačen. , ker pa je osnovna ploskev kvadrat, zapišemo oziroma . Za izračun potrebujemo še , ki pa jo lahko dobimo iz podanega razmerja med osnovnim robom in višino:
ali , lahko pa tudi .
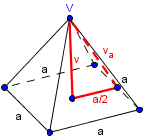
Uporabimo Pitagorov izrek v trikotniku znotraj piramide in podano razmerje ter dobimo:
Višino na osnovnico vstavimo v enačbo za izračun površine piramide, rezultat je:
.
Osni presek stožca
Povlecite ploščine osnih presekov na desni k podatkom stožca na levi.
Napačno
Odgovor je napačen. Osni presek stožca je trikotnik, katerega ploščina je odvisna od dolžine stranic. Ker so stranice stožca vedno enake, je obrazec za izračun ploščine osnega preseka prav tako enak za vse stožce: .
| Gre za enakostranični stožec, njegova površina je . Lahko izračunamo polmer: | Gre za enakostranični stožec: | Iz danih podatkov lahko izračunamo ploščino osnega preseka, saj imamo vse potrebne podatke. | |
Prostornina stožca
Kot pri vrhu osnega preseka stožca meri , stranica stožca pa . Koliko meri prostornina stožca, če jo zaokrožimo na celo število?
Napačno
Odgovor je napačen.
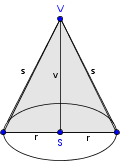
S pomočjo kotne funkcije lahko izračunamo polmer osnovne ploskve stožca, iz tega pa višino in prostornino stožca:
Kroglice
Dve kroglici premera in zlijemo v eno. Kakšen bo njen premer?
Napačno
Odgovor je napačen. Izračunati moramo skupno prostornino kroglic, saj gre za zlitino:
,
,
Skupna prostornina . Iz prostornine izračunamo polmer zlite kroglice:
Ker pa so možni odgovori zapisani s potenco, zapišimo še rezultat s potenco: .
Enakostranični valj in krogla
Enakostraničnemu valju včrtamo kroglo. Kakšno je razmerje površin?
Napačno
Odgovor je napačen. Površina valja
.
Izrazimo lahko polmer krogle: .
Lahko nadaljujemo z računanjem razmerja:
Razmerje med površinama enakostraničnega valja in krogle je .
Rezultati