jsMath

Geometrijski liki in ploščine - teorija

Geometrijski liki in ploščine - teorija

Avtor: Skupina NAUK

Več o projektu...

Lastnosti ploščine

Ploščino posameznih likov bomo označevali z S. Ustrezna enota je kvadratni meter(m2), kvadratni decimeter(dm2), kvadratni centimeter(cm2)... 1m2 predstavlja ploščino kvadrata s stranico 1m. Velja, da imajo skladni liki enako ploščino.

Ploščine in obsegi likov:

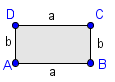
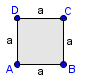
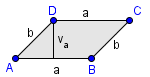
Skica(pravokotnik_pl.png) (kvadrat_pl.png) (paralelogram_pl.png)
LikPravokotnikKvadratParalelogram
PloščinaS=abS=a2S=ava ali S=absinα
Obsego=2a+2bo=4ao=2a+2b

PREMISLITE

Kako bi izračunali ploščino lika nepravilne oblike?

Odgovor

Ploščina lika nepravilne oblike

Če je lik manjši, naredimo njegov odtis na milimetrski papir, preštejemo vse kvadratne centimetre, ki jih lik pokriva, nato preštejemo še vse kvadratne centimetre, ki so skupni z likom, pa niso celi. To sta spodnja in zgornja meja ploščine lika. Postopek ponovimo še s preštevanjem kvadratnih milimetrov, spet dobimo spodnjo in zgornjo mejo ploščine ... Ploščina lika je vmesna vrednost med zgornjo in spodnjo mejo, ki se razlikujeta za malo. Večje like nepravilne oblike pa namesto na milimetrski papir položimo na večje ploskve.

Ploščine-nadaljevanje

Skica(trikotnik_pl.png) (pravokotni_trikotnik_pl.png) (enakostranicni_trikotnik_pl.png) (trapez_pl.png)
LikTrikotnikPravokotni trikotnikEnakostranični trikotnikTrapez
PloščinaS=2ava=2bvb=2cvc ali
S=2cbsinα=2casinβ=2absinγ		S=2abS=4a2√3S=2a+c·v
Obsego=a+b+co=a+b+co=3ao=a+b+c+d

Če sta e in f dolžini diagonal štirikotnika ABCD, ϕ pa kot med njima, potem je ploščina štirikotnika enaka 21efsinϕ (odgovorite še na vprašanje pod PREMISLITE).

PREMISLITE

Pri katerih likih sta diagonali pravokotni?

Odgovor

Pravokotni diagonali likov

Diagonali sta pravokotni pri kvadratu, rombu in deltoidu. Zato je ploščina kvadrata, romba in deltoida

21efsinϕ=21efsin90°=2ef.

Zgledi

1. Koliko meri ploščina trikotnika s podatki c=6cm, a=7cm, β=45°?
Rešitev

Ploščina trikotnika se lahko izračuna tudi z obrazcem S=2casinβ. Ker imamo vse podatke, jih vstavimo v enačbo: S=26·4sin45°=12·2√2=6√2.

2. Dolžini diagonal romba sta v razmerju 2:5, njegova ploščina pa je 180cm2. Koliko merita diagonali?
Rešitev

e=2x, f=5x
S=2ef
180=22x·5x
180=5x2
x2=36
x=6⇒e=12cm in f=30cm.

3. Na vrtu imamo peskovnik dimenzij 150cm x 250cm. Želimo narediti nov peskovnik, ki bo kvadraten in bo zasedel enako prostora. Kakšnih dimenzij mora biti nov peskovnik?

(peskovnik.png)

Rešitev

Ker želimo, da zasede enako prostora, moramo enačiti ploščine peskovnikov. Ploščina sedanjega je S=150·250=37500cm2. Stranica novega je zato a=√S=√37500=193,65cm.

Polmer trikotniku včrtanega kroga

(polmer_vcrtanega_kroga.png)

Središče trikotniku včrtanega kroga je presečišče simetral kotov. Ploščina trikotnika ABC je ploščina treh trikotnikov, ki ga sestavljajo, ploščina △ABS, ploščina △BCS in ploščina △CAS. Zato je ploščina trikotnika ABC enaka

S=2cr+2ar+2br=r2a+b+c=r2o.

Polovico obsega trikotnika označujemo s črko s, zato lahko zapišemo S=rs. Od tod dobimo obrazec za polmer trikotniku včrtanega kroga:

r=sS.

Heronov obrazec

S pomočjo Heronovega obrazca lahko izračunamo ploščino poljubnega trikotnika, če imamo podane vse tri njegove stranice:

S=√s(s−a)(s−b)(s−c), 

kjer je s že prej omenjena polovica obsega trikotnika: s=2a+b+c.

Zgled:

Koliko meri ploščina trikotnika s stranicami a=5cm, b=6cm in c=3cm?

Rešitev

s=25+6+3=7, po Heronu je ploščina triktonika S=√s(s−a)(s−b)(s−c)=√7(7−5)(7−6)(7−3)=√7·2·1·4=√56=.7,5 .

Kolikšen je polmer temu trikotniku včrtanega kroga?

Izračunali smo ploščino trikotnika in s, zato lahko izračunamo polmer:
r=sS=77,5=.1,07cm.

Sinusni izrek

(sinusni_izrek.png)

Če uporabimo kotno funkcijo sinus v trikotniku ABC, dobimo sinα=bvc⇒vc=bsinα. Ploščina trikotnika je enaka polovici zmnožka stranice in višine na stranico: S=2c·vc=2c·b·sinα. Podobno lahko zapišemo tudi za ostala dva kota: S=2a·c·sinβ in S=2a·b·sinγ. Če obrazca enačimo in krajšamo z a2, dobimo enakost csinβ=bsinγ ali bsinβ=csinγ. Enak je tudi količnik asinα. To je sinusni izrek, s pomočjo katerega lahko iz podane stranice in dveh kotov lahko izračunamo ostale stranice:

asinα=bsinβ=csinγ.

Zgled:

Koliko meri kot α v trikotniku s podatki: a=4,5cm, b=5cm, β=45°?
Rešitev

asinα=bsinβ
sinα=basinβ
sinα=34,5·sin82°
sinα=0,636
α=39,5° in α=180°−39,5°=140,5°, ki ne ustreza, saj je α+β>180°.

PREMISLITE

Na kaj moramo paziti pri računanju kotov s pomočjo sinusnega izreka?

Odgovor

Koti pri sinusnem izreku

Pri računanju kotov z uproabo sinusnega izreka moramo paziti, da ne izpustimo kakšne rešitve:
β=arcsinx
β=180°−arcsinx
Na koncu moramo vedno preveriti, če ta rešitev res ustreza.

Polmer trikotniku očrtanega kroga

(polmer_ocrtanega_kroga.png)

Središče trikotniku očrtanega kroga je presečišče simetral stranic. Velja sinγ=c2R. Podobno velja tudi za ostale stranice, zato je

2R=asinα=bsinβ=csinγ.

Če upoštevamo, da je ploščina trikotnika ABC enaka S=21bcsinα, je obrazec za polmer trikotniku očrtanega kroga

R=4Sabc.

PREMISLITE

Kdaj je štirikotnik tetiven?

Odgovor

Kdaj je štirikotnik tangenten?

Odgovor

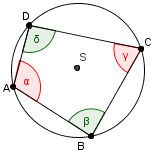
Tetivni štirikotnik

(tetivni_stirikotnik_liki.png)
Tetivni štirikotnik.

Vsak štirikotnik, ki mu lahko očrtamo krog, je tetiven. Zanj velja:

α+γ=β+δ=180°.

Tangentni štirikotnik

(tangentni_stirikotnik_liki.png)
Tangentni štirikotnik.

Vsak štirikotnik, ki mu lahko včrtamo krog, je tangenten. Zanj velja:

a+c=b+d.

Dolžina krožnega loka

Razmerje med obsegom in premerom kroga je enako za vse kroge in to razmerje označimo z grško črko π: od=π. Iz tega lahko dobimo obseg kroga

o=2πr,

kjer je r polmer kroga.

Ker središčnemu kotu 360° ustreza lok 2πr, središčnemu kotu 1° ustreza lok 2πr360°. Poljubnemu središčnemu kotu pa ustreza dolžina krožnega loka

l=πrα180°,

kjer je kot podan v stopinjah.

Kot, pri katerem je krožni lok enak polmeru, se imenuje radian. Celoten krog predstavlja 2π radianov, obrazec za izračun dolžine krožnega loka z radiani pa je

l=rα.

Tabela za pretvarjanje kotov iz stopinj v radiane

Tabela za pretvarjanje kotov iz stopinj v radiane

StopinjeRadiani
360°2π
180°π
90°π2
60°π3
45°π4
30°π6
0°0

Zgledi

1. Koliko meri polmer trikotniku očrtanega kroga pri enakostraničnem trikotniku?
Rešitev

Ploščina enakostraničnega trikotnika je S=4a2√3.

R=4Sabc=a3a2√3=3a√3

2. Če spremenimo kot 150° v radiane, je to
Rešitev

180°150°π=65π

Če spremenimo kot 54π v stopinje, je to
Rešitev

54·180°=144°


3. Koliko meri središčni kot α v stopinjah in radianih, če je dolžina pripadajočega krožnega loka l=6cm in polmerom r=10cm?
Rešitev

Kot v stopinjah:
α=πr180°l=π108°=34,38°.

Kot v radianih:
α=lr=0,6 radianov.

Ploščina kroga in krožnega izseka

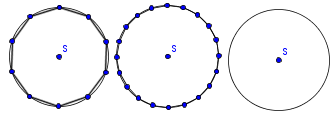
Ploščina kroga je podobna ploščini n-kotnika, ki mu je očrtan krog:

(ploscina_kroga.png)
10-kotnik, 20-kotnik in krog.

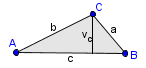
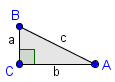
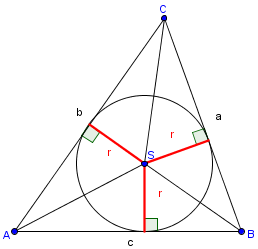
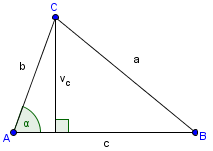
Ploščina enega trikotnika je 2s·v, kjer je s stranica trikotnika, v pa njegova višina. v je podobna polmeru kroga r, s pa, če gledamo ploščino celotnega kroga, obsegu kroga. Zato je ploščina kroga podobna 2o·r=22πr·r=πr2. Ker pa se n-kotnik vedno bolj bliža krogu, ugotovimo, da je ploščina kroga prav taka:

S=πr2.

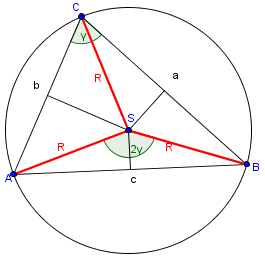
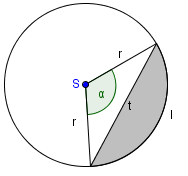
Krožni izsek je množica točk kroga, ki ležijo v danem središčnem kotu:

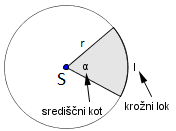
(ploscina_kroznega_izseka.png)

Ploščina krožnega izseka je ploščina dela krožne ploskve in je permosorazmerna s središčnim kotom. Središčnemu kotu 360° pripada celotna ploščina kroga, πr2, zato središčnemu kotu 1° pripada ploščina πr2360°. Poljubnemu kotu α pripada ploščina izseka

S=πr2α360°,
če je kot podan v stopinjah
S=2l·r,
če je kot podan v radianih.

Krožni kolobar in ploščina krožnega odseka

(krozni_kolobar.png)
Krožni kolobar s polmeroma r in R ter debelino a.

Ploščina krožnega kolobarja je ploščina med manjšim in večjim krogom, s središčem v isti točki.
S=πR2−πr2
S=π(R2−r2)
S=π(R−r)(R+r), kjer je R−r debelina kolobarja.

Krožni odsek je množica točk, ki je omejena s krožnim lokom in tetivo nad danim središčnim kotom.

(ploscina_kroznega_odseka.png)

Ploščina krožnega odseka je razlika med ploščino krožnega izseka in trikotnikom ABS, zato lahko zapišemo S=2r2α−2r2sinα

S=2r2(α−sinα)

PREMISLITE

Kako bi izračunali ploščino krožnega odseka, če je središčni kot podan v stopinjah?

Odgovor

Ploščina krožnega odseka, če je kot v stopinjah

Če je središčni kot podan v stopinjah, potem je ploščina krožnega izseka S=πr2α360°. Ploščina trikotnika, ki ga tvorita tetiva in polmera nad tetivo, je S=2t·v. Ploščina krožnega odseka pa je ravno njuna razlika:

S=πr2α360°−2t·v.

Zgledi

1. Polmer večjega kroga je 5cm. Ploščina kolobarja med večjim in manjšim krogom je 16πcm2. Koliko meri polmer manjšega kroga?
Rešitev

S=π(R−r)(R+r)
16π=π(5−r)(5+r)
16=25−r2
r2=4
r=2cm.
Ploščina manjšega kroga meri 2cm.

2. Kolikšna je ploščina pobarvanega dela trikotnika, če je kot α=48° in višina vc=3cm?
Rešitev

(zgled_izsek.png) Iz slike se vidi, da je polmer kroga s središčem v C enak vc. Izračunati je potrebno ploščino krožnega izseka:
S=πr2α360°
S=1,26cm2

3. Koliko krogov iz blaga s polmerom 2,5cm lahko izrežemo iz kvadrata s ploščino 50cm2?
Rešitev

Skroga=πr2=π·2,52=19,63cm2.
Ker je ploščina kvadrata 50cm2, lahko izrežemo iz blaga 2 cela kroga.
0%
0%