Diferencialni račun - vaje
Pravilno ime
Odgovor je pravilen.
Odgovor je napačen. Izraz se imenuje diferenčni količnik. Limita tega količnika pa je odvod.
Grafični pomen
Kaj grafično predstavljata diferenčni količnik in odvod funkcije v dani točki?
Odgovor je pravilen.
Odgovor je napačen. Diferenčni količnik predstavlja naklon sekante, odvod pa naklon tangente.
Velikost h
Ocenite velikost , da bo sekanta skozi točki in približno opisovala naklon krivulje med tema dvema točkama. Pomagajte si z drsnikom na sliki. Pravilnih je več različnih odgovorov.
Če je med (vpišite nižjo vrednost) in (vpišite višjo vrednost), potem premica skozi točki in ponazarja naklon krivulje med tema dvema točkama.
Odgovor je pravilen. Pravilni odgovori so vsi, ki vključujejo med in . Če bi vzeli , potem daljica seka "dolino", če bi vzeli , pa daljica seka "hrib" in se dani krivulji ne prilega več dobro.
Oglejte si to še enkrat na spodnji animaciji:
Odgovor je napačen. Pravilni odgovori so vsi, ki vključujejo med in . Če bi vzeli , potem daljica seka "dolino", če bi vzeli , pa daljica seka "hrib" in se dani krivulji ne prilega več dobro.
Oglejte si to še enkrat na spodnji animaciji:
Kaj je odvod?
Kaj od naštetega predstavlja definicijo odvoda?
Odgovor je pravilen.
Odgovor je napačen. Pravilen odgovor je .
Odvod je limita diferenčnega količnika. Diferenčni količnik pa je .
Odvajanje po definiciji
Dana je funkcija . Funkcijo odvajamo po definiciji . Namesto in vstavimo dano funkcijo. Med ponujenimi odgovori izberite pravilnega.
Odgovor je pravilen.
Odgovor je napačen.
pomeni, da v funkcijo f(x) namesto vseh vstavimo
- dana funkcija je , zato je
ker je v ulomku pred f(x) minus, je pomembno, da ne pozabimo oklepajev
- prvi oklepaj bi lahko spustili, saj ne vpliva na rezultat, drugi oklepaj pa je obvezen . Naprej
Odvod potenčne funkcije
1. Izberite pravilno formulo za odvod potenčne funkcije.
2. Dana je funkcija . Izračunajte vrednost odvoda za
Odgovor:
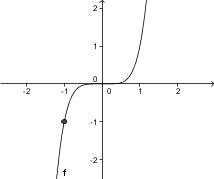
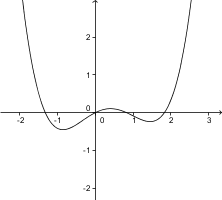
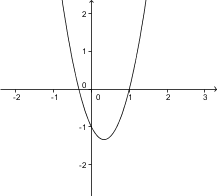
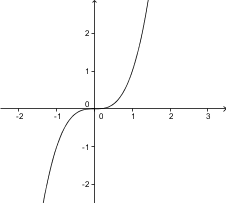
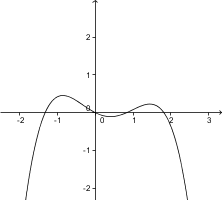
3. Izberite sliko, ki prikazuje izračunano vrednost.
Odgovor je pravilen.
Vsaj eden od odgovorov je napačen.
1. Pravilo za odvod potence je .
2. Do tega rezultata pridemo tako, da funkcijo odvajamo, dobimo in za vstavimo .
3. Pravilna slika je
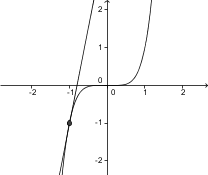
Odvod funkcije v dani točki predstavlja smerni koeficient tangente v tej točki.
Niste odgovorili na vsa vprašanja. Zaprite to okno in preverite svoje odgovore.
Odvodi kotnih funkcij
Povežite!
Odgovor je pravilen.
Vrednost odvoda
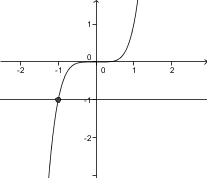
Kakšna je vrednost odvoda v označenih točkah na sliki?
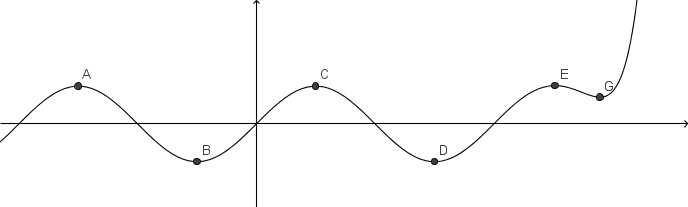
Vrednost odvoda v označenih točkah je enaka .
Odgovor je pravilen.
Odgovor je napačen.
V označenih točkah je vrednost odvoda 0. To se vidi tudi tako, da so tangente na krivuljo v teh točkah vzporedne z osjo.
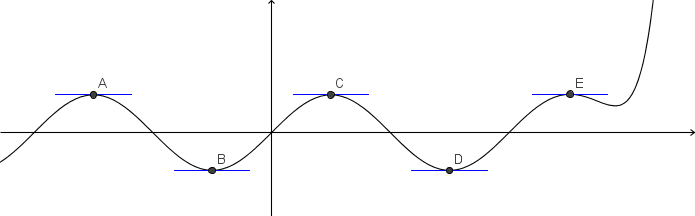
Naraščanje in padanje
Dana je funkcija . Na levi sliki je graf funkcije, na desni sliki je graf odvoda te funkcije. Določite intervale naraščanja in padanja funkcije .
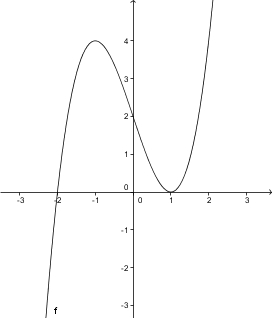
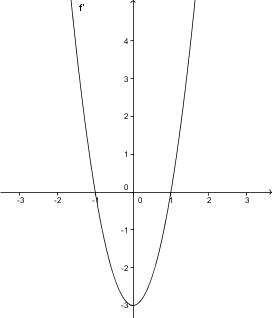
Odgovor je pravilen.
Odgovor je napačen. Funkcija narašča oziroma pada med ekstremalnimi točkami. Na grafu odvoda pa to vidimo tako: kjer je graf odvoda pozitiven, tam funkcija narašča, kjer je negativen, pa pada.


Rešitve:
- - nič od tega
- - f narašča
- - f pada
- - nič od tega
- - f narašča
- - f narašča
- - nič od tega
Ekstremi 1
Razvrstite korake za računanje ekstremov v pravilni vrstni red.
Odgovor je pravilen.
Odgovor ni pravilen. Pravilen vrstni red je naslednji:
- Izračunamo odvod funkcije.
- Odvod izenačimo z 0.
- Izračunamo stacionarne točke.
- Določimo predznak odvoda med stacionarnimi točkami.
- Določimo katere točke so minimumi in katere maksimumi.
Ekstremi 2
Določite največjo vrednost funkcije na intervalu [0, 3].
Odgovor: Največja vrednost na intervalu [0, 3] je
Odgovor je pravilen.
Odgovor je napačen. Največjo vrednost iščemo med lokalnimi maksimumi.
- Funkcijo najprej odvajamo: .
- Odvod izenačimo z nič, da dobimo stacionarne točke:
(delimo z -3)
Stacionarne točke: in - Na danem intervalu [0, 3] je samo . Ugotovimo, da je ta točka maksimum, zato je 4 največja vrednost na intervalu [0, 3].
Ekstremalni problem
Imamo dve števili a in b, katerih vsota je 200. Poišči ti dve števili, tako da bo njun produkt največji.
Odgovor: ,
Katero količino je treba napisati kot funkcijo in jo odvajati?
Odgovor je pravilen.
Odgovor je napačen. Pravilni odgovor je , , za funkcijo proglasimo in odvajamo produkt . Nalogo rešimo takole:
- Iščemo dve števili, tako da bo produkt največji, zato produkt razglasimo za funkcijo.
Iz vsote izrazimo eno izmed spremenljivk, , in jo vstavimo v formulo za produkt.
- Odvajamo :
Rešimo enačbo
- Izračunamo še , .
Niste odgovorili na vsa vprašanja. Zaprite to okno in preverite svoje odgovore.
Težja naloga
Odgovor je pravilen.
Odgovor je napačen.
- Tam, kjer graf odvoda seka os , so ničle odvoda. To pomeni, da je za te . V , za katere to velja, ima funkcija stacionarne točke.
- Kjer je graf odvoda pod osjo , to pomeni, da je tam vrednost odvoda negativna. Negativen odvod pomeni, da je funkcija za tiste padajoča.
- Kjer je graf odvoda nad osjo , to pomeni, da je tam vrednost odvoda pozitivna. Pozitiven odvod pomeni, da je funkcija za tiste naraščajoča.
|
|
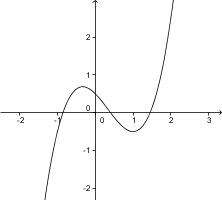
Poglejmo, kako to razberemo na dani sliki:
- Graf odvoda seka os blizu , med in ter med in . To pomeni, da ima graf funkcije v teh točkah stacionarne točke.
- Graf odvoda je za negativen, to pomeni, da graf funkcije za pada.
- Graf odvoda je med prvo in drugo ničlo odvoda (gledano z leve) pozitiven, to pomeni, da graf funkcije med tema dvema točkama (ki sta na grafu funkcije stacionarni točki) narašča.
- Med drugo in tretjo ničlo odvoda (gledano z leve) je graf odvoda negativen, kar pomeni, da graf funkcije med tema dvema točkama pada.
- Od tretje ničle odvoda naprej je graf odvoda pozitiven, kar pomeni, da graf funkcije od tu naprej narašča.
Razmislite, kaj pomeni, kadar je odvod enak 0, kadar je negativen ali pozitiven.
Rezultati