Ploščina pravokotnika meri , njegov obseg pa . Koliko meri krajša stranica pravokotnika?
Geometrijski liki in ploščine - vaje
Geometrijski liki in ploščine - vaje
Skupina NAUK
Urjenje in utrjevanje geometrije v ravnini, likov in ploščin.
Pravokotnik
Napačno
Odgovor je napačen. Iz podatkov lahko izračunamo dolžino stranic pravokotnika:
Rešimo enačbo z eno neznako in dobimo rešitvi in . |
Ker naloga sprašuje po krajši stranici, je le ta dolžine .
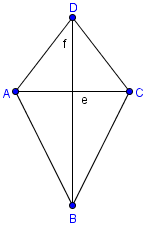
Deltoid
Ploščina deltoida, kjer sta diagonali v razmerju , je . Koliko merita diagonali?
Napačno
Odgovor je napačen. Ker gre za razmerje, zapišemo ali , ali , . Recimo, da uporabimo prvi dve enakosti. Iz podane ploščine deltoida in razmerja diagonal izračunamo dolžini diagonali:
.
Dolžini diagonal sta zato in . Ker pa so rezultati zahtevani v decimetrih, jih je treba še ustrezno pretvoriti. Pravilni odgovori so zato:
ali
Pravilni 7-kotnik
Pravilnemu sedemkotniku je očrtan krog s polmerom . Koliko meri ploščina 7-kotnika, če jo zaokrožite na celo število?
Napačno
Odgovor je napačen. Ploščina sedemkotnika je enaka ploščini sedmih enakokrakih trikotnikov. Najlažje si predstavljamo, če lik skiciramo:
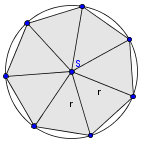
Središčni kot .
Trikotniku včrtan in očrtan krog
Trikotniku s podatki , , očrtamo in včrtamo krog. Kolikšna je razlika med polmeroma trikotniku očrtane in včrtane krožnice? (Razlika naj bo zaokrožena na celo število.)
Napačno
Odgovor je napačen. Pravilna rešitev:
| S Heronovim obrazcem izračunamo ploščino trikotnika: | Polmer trikotniku včrtanega kroga: | Polmer trikotniku očrtanega kroga: |
| , kjer je |
Razlika med polmerom trikotniku očrtane in včrtane krožnice je .
Ploščina trikotnika
Trikotniku s podatki , , izračunajte najprej dolžino vseh stranic, obseg in na koncu še ploščino. Vse rezultate zokrožite na eno decimalko.
Dolžina stranice : cm
Dolžina stranice : cm
Obseg trikotnika: cm
Ploščina trikotnika: cm
Napačno
Odgovor je napačen. S pomočjo sinusnega izreka najprej izračunamo dolžini neznanih stranic:
Obseg trikotnika je vsota vseh treh stranic trikotnika, zato je .
Ploščino trikotnika s podanimi stranicami in koti lahko izračunamo s pomočjo Heronovega obrazca, kjer je ali lažje, z uporabo enega izmed obrazcev za izračun ploščine trikotnika: . Katerikoli način uporabimo, moramo dobiti isti rezultat, .
Krožni lok in izsek
Podan je krog s polmerom in tetivo v njem dolžine . Odgovorite na vprašanja na desni.
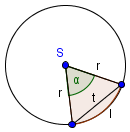
- Koliko meri središčni kot?(rezultat naj bo celo število)
- Koliko meri ploščina krožnega izseka?(rezultat naj bo celo število) cm
- Kolikšna je dolžina krožnega loka, ki je omejen s tetivo?(rezultat zaokrožite na eno decimalko) cm
Napačno
Odgovor je napačen. Ker gre za enakokraki trikotnik, ki ga tvorita polmera kroga in tetiva, lahko za izračun središčnega kota uporabimo kotne funkcije.
Najprej izračunamo kot , središčni kot pa dobimo tako, da ga podvojimo:
. Ker mora biti rezultat celo število, je pravilen odgovor .
Ploščino krožnega izseka izračunamo po obrazcu:
Dolžino krožnega loka izračunamo po obrazcu:
.
Pretvorbe iz stopinj v radiane
Na levi so napisani koti v stopinjah, na desni pa koti v radianih. Povežite med seboj enake kote.
Napačno
Odgovori so napačni. Ker je radianov, je radiana. Zato je:
- radiana
- radiana
- radiana
- radiana
- radiana
- radiana
Ploščina lika 1
Izračunajte ploščino pobarvanega lika.
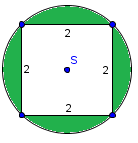
Napačno
Odgovor je napačen. Ploščina pobarvanega lika je enaka razliki med ploščino kroga s središčem v in polmerom polovico diagonale ter ploščino kvadrata. Ker je polovica diagonale kvadrata s stranico enaka , je to polmer kroga. Ploščina lika je zato:
.
Ploščina lika 2
Izračunajte ploščino pobarvanega lika.
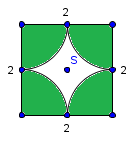
Napačno
Odgovor je napačen. Ploščina pobarvanega lika je enaka razliki med ploščino kvadrata s stranico in štirikratno ploščino četrtine kroga s polmerom . Zato je ploščina pobarvanega lika:
.
Rezultati
