Z miško klikni na točko T in jo premikaj po enotski krožnici. Pri tem opazuj vrednosti sinusa in kosinusa.

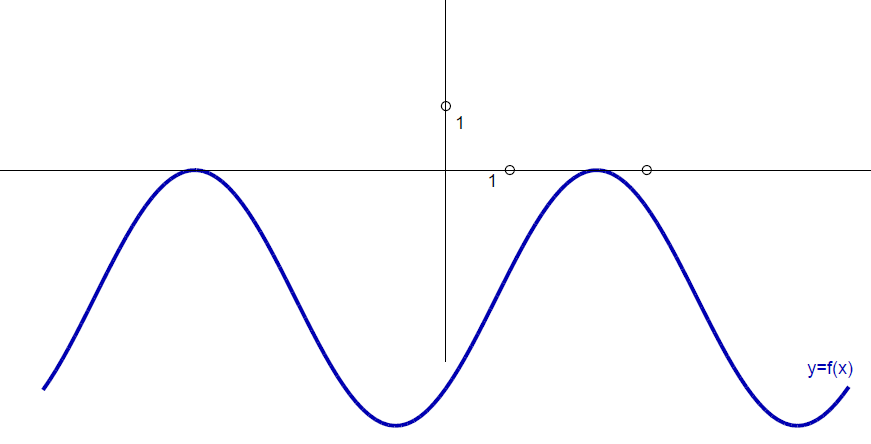
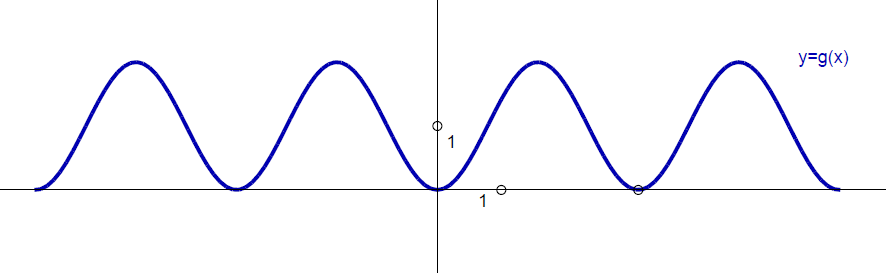
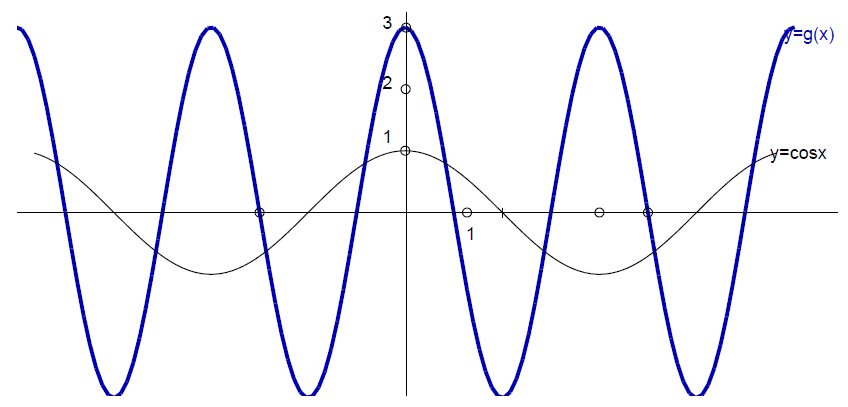
Sinus kota je ordinata točke, v kateri drugi krak kota seka enotsko krožnico, kosinus kota pa je abscisa te točke.

Definicijsko območje sinusa in kosinusa je množica realnih števil, saj lahko poljubnemu kotu poiščemo vrednost sinusa in kosinusa. Obe funkciji sta omejeni, dosežeta lahko le vrednosti med –1 in 1. Torej je zaloga vrednosti interval [–1,1].

Sinus je liha, kosinus pa soda funkcija.

Vrednost sinusa je odvisna od velikosti kota. Graf funkcije sinus bomo narisali tako, da bomo na abscisno os nanašali vrednost kota v radianih, na ordinatno os pa vrednost sinusa.

Spodnja slika nam prikazuje graf funkcije f(x)=sinx, ko spreminjamo kot x radianih od 0 do 2π.

V zgornjem koordinatnem sistemu imamo narisan graf sinusa od 0 do 2π. Vemo, da je funkcija sinus periodična funkcija z osnovno periodo 2π, zato je graf na intervalu od 2π do 4π po obliki enak grafu od 0 do 2π. Prav tako velja za naslednje intervale od 4π do neskončno ter za intervale dolžine 2π levo od izhodišča. Graf funkcije sinus imenujemo sinusoida.

Iz zgornjega grafa funkcije f(x)=sinx so lepo vidne določene lastnosti funkcije sinus, ki jih sicer poznamo že od prej in nam bodo v pomoč pri risanju grafov zahtevnejših funkcij, povezanih s funkcijo sinus.

Izračunajmo ničle, minimume in maksimume funkcije f(x). Pri tem si bomo pomagali z letakom, kjer so opisane lastnosti.

Ničle sinusa nastopijo pri kπ, torej nastopijo ničle funkcije f(x)=sin(3x) pri 3kπ, kjer je k celo število. Podobno s pomočjo letaka dobimo minimume in maksimume. Najdeš jih v spodnji tabeli.

Zapišimo ničle funkcije f(x): ..., –π, –32π, –π3, 0, π3, 32π, π, ...

Maksimumi funkcije so točke, kjer funkcija doseže največjo vrednost. Maksimumi funkcije f(x) so točke T(π6+32kπ,1), kjer je k celo število.

Zapišimo nekaj maksimumov: (−π2,1), (π6,1), (65π,1), (23π,1).

Minimumi funkcije so točke, kjer funkcija doseže najmanjšo vrednost. Minimumi funkcije f(x) so točke T(–π6+32kπ,–1), kjer je k celo število.

Zapišimo še nekaj mimimumov: (−65π,−1), (−π6,−1), (π2,−1), (67π,−1).

Ko imamo izračunanih nekaj točk, ki ležijo na grafu funkcije f(x), lahko narišemo njen graf.

Na zgornji sliki je po korakih prikazana konstrukcija grafa funkcije f(x)=sin(3x). Najprej se na grafu izrišejo ničle, nato minimuni, maksimumi in čisto na koncu krivulja z enačbo y=sin(3x). Poleg te krivulje je še narisan graf funkcije sinus.

S tem, ko neodvisno spremenljivko pomnožimo s konstanto, se spremeni osnovna perioda funkcije. Ohranita se definicijsko območje in zaloga vrednosti funkcije.

Če neodvisno spremenljivko pomnožimo z neko konstanto, opazimo, da se graf funkcije raztegne oziroma skrči v smeri abscisne osi.

Kolikšna je osnovna perioda funkcije f(x)=sin(3x)?
Osnovna perioda funkcije f(x) je:

Preveri

Narišimo graf funckije g(x)=2sinx.

Najprej določi, ničle, minimume in maksimume funkcije g(x).
Ničle nastopijo pri kπ.

Največja vrednost, ki jo doseže funkcija g(x) je 2.
Maksimumi so T(π2+2kπ,2), kjer je k celo število.

Najmanjša vrednost, ki jo doseže funkcija g(x) je –2.
Minimumi so T(–π2+2kπ,–2), kjer je k celo število.

Graf funkcije g(x)=2sinx.

V čem se razlikujeta krivulji y=sinx in y=2sinx?

Ohrani se perioda in definicijsko območje, spremenijo pa se vrednosti sinusa pri istih vrednostih neodvisne spremenljivke. Graf funkcije se raztegne v smeri y osi.

Zaloga vrednosti funkcije g(x) je interval [−2,2].

Z miško spreminjaj vrednosti parametrov A in B in opazuj, kako vplivata na graf funkcije.

S spreminjanjem parametra A se krči oziroma razteza graf funkcije v smei y osi. S tem se spreminja tudi zaloga vrednosti funkcije. Če je |A|>1, se graf raztegne, če pa je |A|<1, se graf skrči. Zaloga vrednosti funkcije f(x)=Asin(Bx) je interval [−A,A].

S spreminjanjem vrednosti parametra B se graf funkcije sinus raztegne oziroma skrči v smeri x osi. S tem se spreminja perioda osnovne funkcije. Če je |B|>1, se graf osnovne funkcije skrči in se perioda zmanjša. Če pa je |B|<1, se graf raztegne, perioda funkcije pa se poveča. Perioda funkcije f(x)=Asin(Bx) je B2π.

Narišimo graf funkcije h(x)=sin(6x+π).

Izračunaj ničle ter vrednosti neodvisne spremenljivke, kjer nastopijo minimumi in maksimumi funkcije h(x).

Iz tabele opazimo, da se vse vrednosti abscis spremenijo za −π6. Torej bo tudi graf po obliki enak, le premakne se v smeri x osi.

Na sliki primerjaj grafa funkcij y=sinx in y=sin(6x+π).

Če neodvisni spremenljivki prištejemo pozitivno realno število a, se graf osnovne funkcije premakne za a v levo v smeri x osi oziroma če odštejemo pozitivno realno število a, se graf osnovne funkcije premakne za a v desno v smeri x osi.

Kako pa se spreminja graf osnovne funkcije, če vrednostim sinusa prištevamo ali odštevamo konstanto? Preveri na spodnji sliki.

Z miško spreminjaj parameter A in pri tem opazuj spreminjanje grafa funkcije.

Če je parameter A pozitivno število, se graf funkcije y=sinx premakne navzgor po y osi, če pa je A negativno število, se graf premakne po y osi navzdol.

Pridobljeno znanje povežimo z že znanim. Se še spomniš transformacij v ravnini?

Imejmo dan graf realne funckije s predpisom f(x). Kako vplivajo parametri A, ω, p in q na graf funkcije g(x)=Af(ω(x–p))+q?

ω ... razteg v smeri x osi,

p ... premik v smeri x osi,

A ... razteg v smeri y osi in

q ... premik v smeri y osi.

Na spodnji sliki sta grafa funkcij f(x) in g(x). Poišči pravilni odgovor.

Preveri

Poglejmo si naslednjo zvezo med sinusom in kosinusa kota:

Torej do grafa funkcije y=cosx pridemo tako, da graf funkcije y=sinx premaknemo za π2 v smeri x osi v levo.

Narišimo graf funkcije f(x)=3cos(x–π3)+1.

Najprej bomo narisali krivuljo y=cosx, nato bomo krivuljo premaknili v desno za π3. S tem dobimo krivuljo z enačbo y=cos(x–π3). V naslednjem koraku bomo upoštevali, da vse vrednosti kosinusa pomnožimo s 3, torej bomo narisali krivuljo y=3cos(x–π3). V zadnjem koraku bomo upoštevali še prišteto konstanto 1, torej prestavimo graf za eno enoto po y osi navzgor. S tem dobimo graf funkcije g(x).

Na spodnji sliki se po korakih izrisujejo posamezne krivulje:

y=cosx,

y=cos(x–π3),

y=3cos(x–π3),

y=3cos(x–π3)+1.

Dana je funkcija s predpisom:

a) Zapiši definicijsko območje in zalogo vrednosti funkcije f(x).

Preveri

b) Izračunaj vrednosti neodvisne spremeljivke, kjer funkcija f(x) doseže minimume in maksimume.

Preveri

c) Nariši graf funkcije f(x).

Rešitev

Nariši graf funkcije podane s predpisom g(x)=−cos(2x)+1.

Rešitev

Zapiši periode funkcij.

Preveri

Zapiši predpis za funkcijo g(x), katere graf je na slliki. Graf funkcije g(x) dobiš z raztegoma funkcije y=cosx v smeri koordinatnih osi.

Preveri