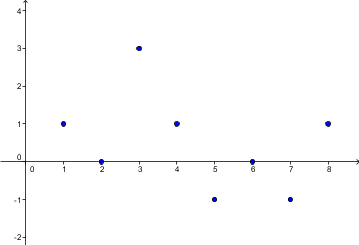
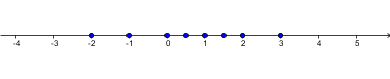
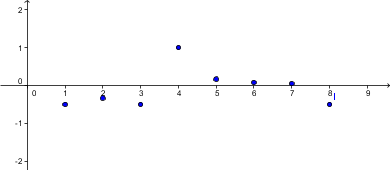
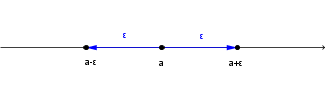
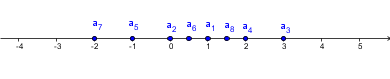Zaporedje pomeni, da imamo neke elemente postavljene v vrsto. Pri tem točno vemo, na katerem mestu v vrsti je kateri element. V matematiki nas zanimajo številska zaporedja (elementi, ki jih postavljamo v vrsto, so števila). Formalno to definiramo takole:
To pomeni, da imamo neko funkcijo , recimo . Vrednosti funkcije dobimo tako, da za vstavljamo vrednosti iz množice . Če vstavljamo vrednosti po vrsti od 1 naprej, dobimo zaporedje:
Če pa nas zanima element na nekem poljubnem mestu v zaporedju, vstavimo številko tega mesta v funkcijo in dobimo vrednost: če nas zanima element na 1991 mestu, izračunamo .
Ker je zaporedje posebna funkcija, namesto oznake uporabljamo oznako . Vrednosti , , , ... so členi zaporedja, pa imenujemo splošni člen.